ミロのブログ

カテゴリー: Mathematics

  • 順序統計量

    順序統計量に関する備忘録.

    ここでは単に確率変数と言えば実数値をとるものとし, 確率変数 \(X\) に対して, その分布関数(distribution function)とは

    \[F_X(x)=\mathrm{Pr}[X\leq x]\]

    で定義される \(F_X:\mathbb{R}\to[0,1]\) のこととします.

    独立同分布な確率変数 \(X_1,\ldots,X_n\) が与えられたとき, それらを小さい順に並べ替えたもの

    \[X_{(1)}\leq X_{(2)}\leq \cdots\leq X_{(n)}\]

    を順序統計量(order statistics)と言います. 特に各 \(1\leq i\leq n\) について, \(X_{(i)}\) を 第 \(i\) 順序統計量 ( \(i\) th static order) と言います.

    主に重要な定理は次です.

    定理

    独立同分布な確率変数 \(X_1,\ldots,X_n\) が与えられており, それらの分布関数が \(F:\mathbb{R}\to[0,1]\) であるとする. すると, 第 \(i\) 順序統計量 \(X_{(i)}\) の分布関数は

    \[F_{X_{(i)}}(x)=\sum_{j=i}^n\binom{n}{j}F(x)^j(1-F(x))^{n-j}\]

    で与えられる. 特に \(X_1\) が密度関数 \(f\) をもてば, 各 \(X_{(i)}\) も密度関数 \(f_{X_{(i)}}\) をもち,

    \[f_{X_{(i)}}(x)=i\binom{n}{i} F(x)^{i-1}(1-F(x))^{n-i}f(x)\]

    が成立する.

    証明

    各 \(1\leq i\leq n\) と \(x\in\mathbb{R}\) について,

    \(\begin{align}\Pr[X_{(i)}\leq x]&=\Pr[X_1,\ldots,X_n の中のすくなくとも i 個が x 以下]\\&=\sum_{j=i}^n\Pr[X_1,\ldots,X_n の中のちょうど j 個が x 以下]\\&=\sum_{j=i}^n\binom{n}{j}F(x)^j(1-F(x))^{n-j}\end{align}\)

    より前半が従う. 後半は絶対連続性が積や和で保たれることから \(F\) が絶対連続であれば, \(F_{X(i)}\) もそうであり,

    \(\begin{align}f_{X(i)}(x)&=\frac{d}{dx}\sum_{j=i}^n\binom{n}{j}F(x)^j(1-F(x))^{n-j}\\&=\sum_{j=i}^{n-1}\left(j\binom{n}{j}F(x)^{j-1}(1-F(x))^{n-j}f(x)\right.\\&\left.-(n-j)\binom{n}{j}F(x)^j(1-F(x))^{n-j-1}f(x)\right)\\&+nF(x)^{n-1}f(x)\\&=i\binom{n}{i}F(x)^{i-1}(1-F(x))^{n-i}f(x)\\&+\sum_{j=i}^{n-1}\left((j+1)\binom{n}{j+1}F(x)^{j}(1-F(x))^{n-j-1}f(x)\right.\\&\left.-(n-j)\binom{n}{j}F(x)^j(1-F(x))^{n-j-1}f(x)\right)\\&=i\binom{n}{i} F(x)^{i-1}(1-F(x))^{n-i}f(x)\end{align}\)

    となるので, 示したいことが得られる.

  • ラグランジュの反転公式

    逆写像定理とラグランジュの反転公式と呼ばれる逆関数を元の関数を使って陽に書く公式について書きます. 複素解析学の基本的な知識を仮定します.

    逆写像定理

    せっかくなので逆写像定理から証明していきましょう. 逆写像定理の証明と言えば不動点定理あるいはほとんど同じことですがNewton法で各点に対応する逆関数の点を探すという証明が有名ですが, 1変数の正則関数の場合にはRoucheの定理を経由した奇麗な証明があるので, そちらを見ていきましょう.

    まず, 今回用いる道具であるRoucheの定理について復習しておきましょう. よく知られた定理なので証明は省略します.

    定理[Roucheの定理]

    \(U\subset\mathbb{C}\) を空でない単連結開集合, \(C\subset U\) を区分的に滑らかな閉曲線とし, \(f,g:U\to\mathbb{C}\) を定数でない正則関数とする. このとき, \(C\) 上のすべての点 \(z\in C\) で \(|f(z)|>|g(z)|\) が成立すれば, \(C\) の内部における \(f(z)\) と \(f(z)+g(z)\) の零点の個数は(位数の重複も含めて数えれば)一致する.

    補題1

    \(U\subset\mathbb{C}\) を空でない開集合, \(f:U\to\mathbb{C}\) を正則関数とする. \(z_0\in U\) に対して, \(f'(z_0)\neq 0\) が成立するとし, \(w_0=f(z_0)\) としよう. このとき, \(z_0\) を中心とする開円板 \(V\) で \(\overline{V}\subset U\) なるものと \(w_0\) を中心とする開円板 \(W\) が存在して, 任意の \(w\in W\) に対して \(f(z)=w\) となる \(z\in V\) が一意に存在する.

    証明

    \(f'(z_0)\neq 0\) なので, \(f(z)-w_0\) は \(z_0\) で \(1\) 位の零点をもつ. 零点の孤立性から十分小さい \(\varepsilon>0\) をとれば, \(\{z\in\mathbb{C}:|z-z_0|=\varepsilon\}\subset U\) かつ \(|z-z_0|\leq \varepsilon\) において \(f(z)-w_0\) は \(z_0\) 以外の零点をもたないようにすることができる.

    \[m=\min_{z\in\{z\in\mathbb{C}:|z-z_0|=\varepsilon\}}|f(z)-w_0|\]

    とおこう. なお最小値の存在は上式がコンパクト集合上の連続関数の最小化になっていることから従う. 定め方から \(m>0\) である. 今\(V=\{z\in\mathbb{C}:|z-z_0|<\varepsilon\}\) および \(W=\{w\in\mathbb{C}:|w-w_0|<m\}\) とおこう. すると, 任意の \(w\in W\) に対して,

    \(\begin{align}|(f(z)-w)-(f(z)-w_0)|&=|w-w_0|\\ &<m\\ &\leq |f(z)-w_0|\end{align}\)

    となる. ゆえに Roucheの定理から \(f(z)-w_0\) と\(f(z)-w=(f(z)-w)-(f(z)-w_0)+(f(z)-w_0)\) の\(V\) での零点の個数は一致し, これはちょうど \(1\) つである. ゆえに任意の \(w\in W\) に対して, ただ一つの \(z\in V\) が存在して, \(f(z)=w\) となる.

    補題2

    補題1と同じ状況の下, \(z_0\) の開円板 \(V\) と \(w_0\) の開円板 \(W\) の間に逆写像 \(g=f^{-1}:W\to V\) が定まる. \(C=\partial V\) を \(U\) における \(V\) の境界のなす円周とすると, \(g\) は積分表示

    \[g(w)=\frac{1}{2\pi i}\int_C \zeta\frac{f'(\zeta)}{f(\zeta)-w}d\zeta\]

    をもつ. 特に \(g\) は \(W\) 上正則である.

    証明

    まず, 補題1の証明から\(w\in W\)を固定するごとに \(C\) 上では

    \[|f(\zeta)-w|\geq |f(\zeta)-w_0|-|w-w_0|>0\]

    なので, この積分で分母が0になることはなく, 積分は問題なく定義されることに注意しておく.

    \(w\in W\) を固定する. このとき, \(U\) 上の正則関数\(f(z)-w\) は \(V\) 上で\(1\) 位の零点をもつから \(\frac{(f(z)-w)’}{f(z)-w}=\frac{f(z)’}{f(z)-w}\) の \(V\) の中での極は \(g(w)\) で\(1\)位のみであり, \(\zeta\mapsto\zeta\frac{f'(\zeta)}{f(\zeta)-w}\) の \(z=g(w)\) での留数は \(g(w)\) なので, 留数定理から積分表示

    \[g(w)=\frac{1}{2\pi i}\int_C \zeta\frac{f'(\zeta)}{f(\zeta)-w}d\zeta\]

    が従う. \(g\) の正則性は \(W\) の中の任意の区分的に滑らかな単純閉曲線 \(\gamma\) に対して, \(C\times\gamma\) 上で関数 \((\zeta,\eta)\mapsto\zeta\frac{f'(\zeta)}{f(\zeta)-\eta}\) は有界な連続関数となり, しかも \(\zeta\in C\) を固定するごとに \(\gamma\) の内部で \(\eta\) について正則である. 以上からFubiniの定理とCauchyの積分定理を用いて,

    \[\int_\gamma g(\eta)d\eta=\frac{1}{2\pi i}\int_C\int_\gamma \zeta\frac{f'(\zeta)}{f(\zeta)-\eta}d\eta d\zeta=0\]

    となるので, \(\gamma\) の任意性から Moreraの定理により従う.

    以上をまとめて逆写像定理が従います.

    定理[逆写像定理(Inverse Function Theorem for Holomorphic Functions)]

    \(U\subset\mathbb{C}\) を空でない開集合, \(f:U\to\mathbb{C}\) を正則関数とする. \(z_0\in U\) に対して, \(f'(z_0)\neq 0\) が成立するとし, \(w_0=f(z_0)\) としよう. このとき, \(z_0\) を中心とする開円板 \(V\) で \(\overline{V}\subset U\) なるものと \(w_0\) を中心とする開円板 \(W\) が存在して, \(f|_V\) は双正則, すなわち正則かつ逆写像が存在して, 逆写像も正則になる.

    ラグランジュの反転公式

    逆写像定理から正則関数 \(f: U\to\mathbb{C}\) が与えられたとき, \(z_0\in U\) に対して \(f'(z_0)\neq 0\) であれば, \(z_0\) のある開近傍\(V\subset U\) 上で \(f|_V\) は双正則になります. このとき, \(g=(f|_V)^{-1}\) としたときに \(g\) の \(z_0\) での冪級数展開を \(f\) を用いて書くというのが, ラグランジュの反転公式のモチベーションになります.

    定理[ラグランジュの反転公式(Lagrange’s Inversion Formula)]

    \(U\) を\(0\) を含む開近傍とし, \(f:U\to\mathbb{C}\) を正則関数とする. このとき, \(f\) の \(0\) のまわりでの冪級数展開 \(f(z)=\sum_{n=0}^\infty a_nz^n\) の \(z^n\) の係数 \(a_n\) のことを \([z^n](f(z))\) と書くことにする. \(f(0)=0\) を仮定する. もし \(f'(0)\neq 0\) であれば, 適切に近傍を取り直すことで \(f\) は逆写像 \(f^{-1}\) をもち, \(f^{-1}\) も \(0\) のまわりで正則で, 各 \(n\geq 1\) に対して,

    \[[z^n](f^{-1}(z))=[z^{n-1}]\left(\frac{z^n}{nf(z)^n}\right)\]

    が成立する.

    証明

    まず一般にCauchyの積分公式から

    \[[z^n](f(z))=\frac{1}{2\pi i}\int_C\frac{f(\zeta)}{\zeta^{n+1}}d\zeta\]

    が成立する. ここで, \(C\) は\(0\) を含む適当な円周である. さて, \(f\) の逆関数 \(g\) は適当な開近傍において, \(0\) のまわりの適当な円周 \(C\) により

    \[g(w)=\frac{1}{2\pi i}\int_C\zeta\frac{f'(\zeta)}{f(\zeta)-w}d\zeta\]

    と書けたことを思い出そう. すると, 補題1の証明から \(C\) 上で常に \(|f(\zeta)|>|w|\) となるような閉路 \(C\) と \(g\) の定義域をとれたから, このような取り方のもと,

    \(\begin{align} g(w)&=\frac{1}{2\pi i}\int_C\frac{1}{1-\frac{w}{f(\zeta)}}\frac{\zeta f'(\zeta)}{f(\zeta)}d\zeta\\ &=\frac{1}{2\pi i}\int_C\frac{\zeta f'(\zeta)}{f(\zeta)}\sum_{n=0}^\infty\left(\frac{w}{f(\zeta)}\right)^nd\zeta\\ &= \sum_{n=0}^\infty\left(\frac{1}{2\pi i}\int_C\frac{\zeta f'(\zeta)}{f(\zeta)^{n+1}}d\zeta\right)w^n\end{align}\)

    なので, \(n\geq 1\) に対して,

    \(\begin{align}[z^n](f^{-1}(z))&= \frac{1}{2\pi i}\int_C\frac{\zeta f'(\zeta)}{f(\zeta)^{n+1}}d\zeta\\ &=-\frac{1}{2\pi in}\int_C\zeta\left(\frac{d}{d\zeta}\frac{1}{f(\zeta)^n}\right)d\zeta\\ &=-\frac{1}{2\pi in}\int_C\left(\frac{d}{d\zeta}\frac{\zeta}{f(\zeta)^n}\right)d\zeta+\frac{1}{2\pi in}\int_C\frac{d\zeta}{f(\zeta)^n}\\ &=\frac{1}{2\pi i}\int_C\frac{d\zeta}{nf(\zeta)^n}\\&=\frac{1}{2\pi i}\int_C\frac{1}{\zeta^n}\frac{\zeta^nd\zeta}{nf(\zeta)^n}\\ &=[z^{n-1}]\left(\frac{z^n}{nf(z)^n}\right)\end{align}\)

    となって示したいことが得られる.

  • グラフ理論入門

    グラフ理論入門

    グラフ理論の入門記事のまとめ

    1. グラフの性質と基本的性質
      グラフの定義と次数や連結性, パスなどの基本的な性質を確認しています.
    グラフの定義と基本的性質

  • グラフの定義と基本的性質

    グラフの定義と基本的性質

    グラフ理論入門の第1回になります. この記事ではグラフの基本的な用語と例について確認しておきます.

    目次

    1. グラフの定義
    2. *隣接行列と接続行列
    3. 次数と握手補題
    4. パス, 歩道, 閉路
    5. 連結性
    6. 代表的なグラフ
    7. 計算機におけるグラフの表現
    8. 演習問題
    9. プログラミング演習

    *がついているところは予備知識(今回だと線形代数)が必要なところです. 知らない場合は飛ばしても大丈夫です.

    グラフの定義

    ラフに言えば, グラフとは点という対象に対して, 辺を結びそれらを関連付けたものです. この素朴な定義のおかげで, グラフという構造は地図やネットワーク, 電気回路などの実世界の様々なところに出現します. より形式的にはグラフは以下で定義されます.

    定義[グラフ]

    有限集合 \(V\) に対して,

    \[\binom{V}{2}=\{e\subset V:|e|=2\}\]

    と定める. すなわち \(\binom{V}{2}\) とは \(V\) の\(2\)つの要素からなる部分集合全体である. \(V\) と \(\binom{V}{2}\) の部分集合 \(E\subset\binom{V}{2}\) の組

    \[G=(V,E)\]

    をグラフ(graph)という. 各 \(v\in V\) のことは頂点(vertex, node)といい, 各 \(e\in E\) のことは 辺(edge) と呼ばれる. 以降, 相異なる\(2\)頂点 \(u,v\in V\) に対して, \(\{u,v\}\in\binom{V}{2}\) のことを \(uv\) と書くことにする. また, \(V,E\) はそれぞれ \(G\) の 頂点集合(vertex set), 辺集合 (edge set) と呼ばれ, \(V(G),E(G)\) などと書く場合もある.

    \(2\)頂点 \(u,v\in V\) に対して \(uv\in E\) であるとき, \(u,v\) は 隣接(adjacent) しているといい, 逆に\(e=uv\in E\) に対して, \(e\) は\(u\), \(v\) に 接続(incident) しているという. また, \(u,v\) を \(e\) の 端点(end points) という. また, \(e=\{u,v\}\) のとき集合 \(\{u,v\}\)のことを \(e\) の 境界(border) といい, \(\partial e\) と書く.

    補足

    ここでいうグラフは広義には無向単純有限グラフ(undirected-simple-finite graph)と呼ばれるものです. これはより広義にはグラフの辺に向きがあったり, 同じ頂点を結ぶ辺があったり, 同じ端点をもつ辺が複数ある場合もグラフと呼ぶからです. また頂点集合が無限集合になるものも当然考えられ, そういったものは無限グラフ(infinite graph)と呼ばれますが, 取り扱い方やモチベーションが大きく変わってきます.

    隣接することと接続することは似ている定義なので注意してください.

    あまりグラフが集合としてどのように実装しているかを気にする必要はないことは注意しておきます. 例えば, 今回はグラフの定義の都合上, 辺とその境界が同じ集合を指すことになっていますが, あくまでグラフの数学的な”実装”をそのようにしたくらいに考えてもらって結構です. つまり, 辺が端点の2元集合として実現されていることを意識する場面は以降一切ないです.

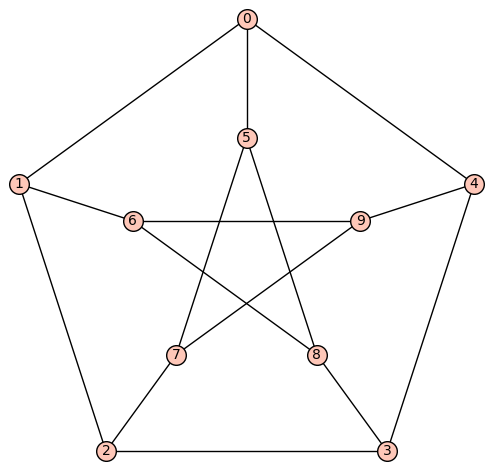
    むしろグラフは下の画像のようにノードを辺で結んだようなものとして視覚的, 幾何学的に理解するべきでしょう.

    なお, このグラフを形式的に書き直せば, 頂点集合が

    \[\{0,1,2,3,4,5,6\}\]

    で辺集合が

    \[\{\{0,1\},\{1,2\},\{3,4\},\{4,5\},\{5,6\},\{3,6\}\}\]

    となります.

    グラフを考えるときの関心ごとは辺のつながり方です. このことから, グラフの同一性は以下の定義を採用することが自然でしょう.

    定義[グラフの同型]

    グラフ \(G=(V(G),E(G)), H=(V(H),E(H))\) に対して, \(\varphi:V(G)\to V(H)\) が 準同型写像(homomorphism) であるとは, 任意の \(u,v\in V(G)\) に対して \(uv\in E(G)\) であれば, \(\varphi(u)\varphi(v)\in E(H)\) となることをいう.

    準同型写像\(\varphi\) が全単射であり, しかも逆写像\(\varphi^{-1}\) が \(H\) から \(G\) への準同型写像になっているとき, \(\varphi\) を 同型写像(isomorphism) といい, グラフ \(G\) と \(H\) の間に同型写像が存在するとき, \(G\) と \(H\) は同型(isomorphic)であるという. このとき, \(G\simeq H\) などと書く.

    *隣接行列と接続行列

    この節の内容は線形代数に詳しくないという方は読み飛ばしてもらっても差し障りないです.

    グラフのデータを管理するために数学的によく用いられるものは隣接行列と接続行列です.

    定義[隣接行列, 接続行列]

    グラフ \(G=(V,E)\) に対して, \(V=\{v_1,\ldots,v_n\},E=\{e_1,\ldots,e_m\}\) と \(V,E\) の元をラベル付けしておく. このとき, 隣接行列(adjacent matrix) \(A_G=(a_{ij})\) とは \(n\times n\) 行列で, その\((i,j)\) 成分が以下で定義されるもののことをいう.

    \[a_{ij}=\begin{cases} 1 &(v_iv_j\in E)\\ 0&(\mathrm{otherwise})\end{cases}\]

    また, \(G\) の 接続行列(incident matrix) \(B_G=(b_{ij})\) とは, サイズ\(n\times m\) の行列でその \(b_{ij}\) 成分が

    \[b_{ij}=\begin{cases} 1 & (v_i\in \partial e_j)\\ 0 &(\mathrm{otherwise})\end{cases}\]

    となる行列のことをいう.

    隣接行列, 接続行列の係数体はここでは特に指定していませんが, 文脈に応じて察せられることがほとんどです. 大抵は二元体 \(GF(2)\) か, 実数体 \(\mathbb{R}\) になると思います.

    また, 今回は頂点や辺にラベルをつけましたが, 文脈によってはラベル付けは行わずに成分を直接頂点集合\(V\) や辺集合 \(E\) で添え字づけることも多いです.

    次数と握手補題

    グラフを調べるうえで最も基本的な量は頂点の次数です. これは, 各点のまわりにどれくらいの点があるのかを見る量です. 当然一般のグラフには極端に多くの点と隣接する点がある一方で, ほとんどの点が近くにないといった頂点があり得ます. しかし, グラフの次数の平均はある程度制約を受けます. これが握手補題と呼ばれ, グラフ理論において最も基本的な道具の一つになります. まずは次数を定義しましょう.

    定義[次数, 正則グラフ]

    グラフ \(G=(V,E)\) が与えられたとき, \(v\in V\) に対して,

    \[\mathrm{deg}_G(v)=|\{e\in E:v\in\partial e\}|\]

    を\(v\) の 次数(degree) という. なお, \(G\) が明らかな場合は \(\mathrm{deg}(v)\) などと略記する.

    自然数\(d\) に対して, グラフ \(G=(V,E)\) が \(d\)-正則(\(d\)-regular) であるとは, すべての \(v\in V\) が \(\deg_G(v)=d\) を満たすことをいう. \(d\) を明記する必要がないときは単に 正則グラフ(regular graph) という. すなわち正則グラフとはすべての点での次数が同じようなグラフである.

    握手補題は次数の平均を正確に見積もります. より正確にどのようなグラフであっても平均次数は\(2|E|/|V|\) になることがわかります.

    定理[握手補題(handshaking lemma)]

    グラフ \(G=(V,E)\) に対して, 次式が成立する.

    \[2|E|=\sum_{v\in V}\mathrm{deg}_G(v)\]

    証明はいわゆる二重数え上げ(double counting)と呼ばれる手法に依ります. 以下に証明を2つ用意していますが, どちらも本質的には同じことをしています.

    証明1

    各頂点 \(v\in V\) に対して,

    \[E_v=\{e\in E:v\in\partial e\}\]

    とおく. 明らかに \(\deg_G(v)=|E_v|\) である. 一方各辺\(e\in E\) に対して, \(e\in E_v\) であることと \(v\in\partial e\) となることは同値なので, \(V=\{v_1,\ldots,v_n\}\) と \(V\) の要素を列挙したときに, 各 \(e\in E\) は \(E_{v_1},\ldots,E_{v_n}\) の中でちょうど2回だけ出現する. 以上から

    \[2|E|=\sum_{v\in V}|E_v|=\sum_{v\in V}\deg_G(v)\]

    となる.

    証明2

    接続行列 \(B_G=(b_{ij})\) の成分の和を考える. 簡単のため \(B_G\) の各成分の添え字は頂点 \(v\in V\) と辺 \(e\in E\) で添え字付けて\(B_G=b_{ve}\) と書こう. すると,

    \[\sum_{v\in V}\sum_{e\in E}b_{ve}=\sum_{v\in V}\deg_G(v)\]

    となる一方,

    \[\sum_{e\in E}\sum_{v\in V}b_{ve}=\sum_{e\in E}2=2|E|\]

    となって, \(2|E|=\sum_{v\in V}\deg_G(v)\) が得られる.

    パス, 歩道, 閉路

    グラフ上を渡り歩いていくようなイメージを定式化したパスやサイクルといったものを定義します. これらもグラフを調べる上で基本的な道具になります. 最初は定義が混乱しがちですが要約すると,

    • 歩道: 何回も同じ頂点を通って良い.
    • パス: 同じ頂点は一度までしか通れない.
    • 閉路: 最初と最後を除いて同じ頂点は一度までしか通れない.

    となります. 注意してください.

    定義[歩道, パス, 閉路]
    グラフ \(G=(V,E)\) が与えられたとき,

    1. 頂点の列 \(W = v_1,v_2,\ldots,v_m\) で, 各 \(1\leq i<m\) に対して, \(v_iv_{i+1}\in E\) となるものが与えられたとき, \(W\) を \(G\) の 歩道(walk) という.
    2. 歩道 \(P = v_1,v_2,\ldots,v_m\) の中で各頂点が高々一度しか出現しないものを パス(path) という.
    3. 歩道 \(C=v_1,\ldots,v_{m+1}\) であって, \(v_1=v_{m+1}\) かつ \(v_1,\ldots, v_{m-1}\) の中に同じ頂点が一度も出現しないものを 閉路(cycle) という.
    4. 上述の歩道, パス, サイクルにおいて \(m\) を歩道, パス, サイクルそれぞれの 長さ(length) という.
    5. 上述の歩道, パスにおいて\(v_1,v_m\) はそれぞれ歩道 \(W\), パス \(P\) の 端点(endpoint) という. 特に端点を明記したい場合は \(v_1\) と \(v_m\) を結ぶパス(path between \(v_1\) and \(v_m\)) などという言い方をする. 歩道についても同様である.

    連結性

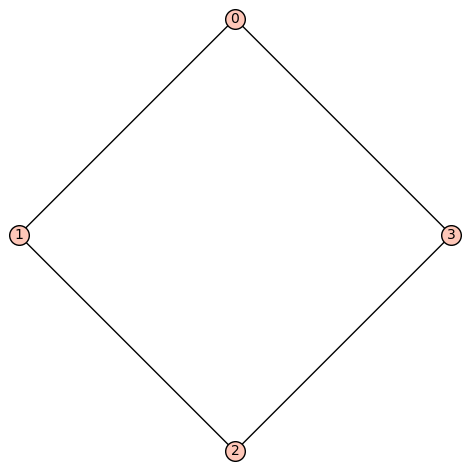
    グラフの定義から以下のようなものもグラフと呼べます.

    しかし, 基本的にはこのようなグラフはつながっているところ, つまり画像の例だと \(\{0,1,2\}\) と \(\{3, 4\}\) で分けて別のグラフと思った方が都合の良いことが多いです. このように”つながっている”という感覚を定式化しておきましょう.

    定義[連結性]
    グラフ \(G=(V,E)\) が 連結(connected) であるとは, 任意の \(u\in V\) と \(v\in V\) に対して, \(u\) と \(v\) を結ぶパスが存在することをいう. 連結でないグラフは 非連結(non-connected) であるという. なお, 1点からなるグラフは常に連結と考える.

    グラフが与えられれば, それらをつながっているところで分割できます. それらのつながった各部分は連結成分といいますが, グラフに関する命題は頂点数に関する帰納法を用いることも多いので, 非連結であることを言えれば, 連結成分ごとで帰納法が適用できたりします.

    定理[連結成分]
    グラフ \(G=(V,E)\) に対して, 頂点と辺の分割

    \[V=V_1\cup V_2\cup\cdots\cup V_k\]

    \[E=E_1\cup E_2\cup\cdots\cup E_k\]

    であって, 以下を満たすものがただ一つ存在する.

    1. 各 \(1\leq i\leq k\) と \(e\in E_i\) に対して, \(\partial e\subset V_i\).
    2. 各\(1\leq i\leq k\)に対して, グラフ\(V_i,E_i\)は連結である.

    このような分割の各 \(V_i\) またはグラフ\((V_i,E_i)\) のことを\(G\) の連結成分(connected component) といい, 各 \(v\in V\) に対して \(v\in V_i\) となるただ一つの \(V_i\) を \(v\) の属する連結成分という.

    なお, 集合 \(X\) の部分集合族 \(\{Y_\lambda\}_{\lambda\in\Lambda}\) が \(X\) の分割であるとは, \(X=\bigcup_{\lambda\in\Lambda} Y_\lambda\) かつ \(\lambda\neq\mu\) ならば \(Y_\lambda\cap Y_\mu=\emptyset\) となるようなもののことをいう.

    証明

    \(V\) 上に同値関係\(\sim\) を

    \[v\sim u\Leftrightarrow v\mbox{ と }u\mbox{ を結ぶパスが存在する}\]

    と定めて, \(V\) の分割を\(\sim\) による商集合 \(V/\sim\) とすればよい. これが本当に同値関係を与え, それによる分割が条件を満たすことは簡単に確かめられる.

    代表的なグラフ

    まず記号を準備しておきます.

    • 正整数\(n\) に対して, \([n]=\{1,2,\ldots,n\}\).
    • 集合 \(X\) と非負整数 \(k\) に対して, \(\binom{X}{k}=\{A\subset X: |X|=k\}\)

    と定めます. これらは少なくとも離散数学の分野に限れば比較的一般的な記号です.

    この節ではいくつか具体例として有用になるグラフの族を挙げておきます. 具体的には以下のものを紹介します.

    完全グラフ

    正整数 \(n\) に対して,

    \[K_n=([n],\binom{[n]}{2})\]

    で定まるグラフを完全グラフ(complete graph)と言います. つまり完全グラフとはすべての頂点の間に辺があるという, ある意味最も極端なグラフです.

    \(K_5\)
    \(K_6\)

    閉路グラフ

    3以上の整数 \(n\) に対して, 閉路グラフ(cycle graph) \(C_n\) とは, 以下で定まるグラフです.

    \[C_n=([n],\{\{1,2\},\{2,3\},\ldots,\{n-1,n\},\{n,1\}\})\]

    つまり, \(C_n\) は長さ\(n\) のサイクルからなるグラフです. 定め方から \(C_3 = K_3\) です.

    \(C_5\)
    \(C_8\)

    ハイパーキューブグラフ

    非負整数 \(n\) に対して, \(Q_n\) で頂点集合が \(\{0,1\}^n\) であり, 辺集合が \(x,y\in\{0,1\}^n\) に対して, \(xy\in E(Q_n)\) となるのが \(x\) と \(y\) のうちちょうど一つの成分だけが異なるとき, かつその時に限るとして定まるグラフを表すものとします. これを ハイパーキューブグラフ(hypercube graph) といいます.

    なお, 似たような名前を持つグラフとして, 3-正則グラフのことをキュービックグラフ(cubic graph) ということがあるので, 混乱しないように注意してください.

    \(Q_3\)

    クネーザーグラフ

    \(n,k\) を非負整数で, \(2k\leq n\) とします. クネーザーグラフ(Kneser graph) \(KG_{n,k}\) とは頂点集合が\(\binom{[n]}{k}\)であり, 辺は \(A,B\in\binom{[n]}{k}\) に対して, \(A\cap B=\emptyset\) であるとき, かつそのときに限り\(AB\in E(KG_{n,k})\) として定まるグラフです.

    特に \(KG_{5,2}\) は ペテルセングラフ(Petersen graph) と呼ばれるグラフで度々グラフ理論において反例として出現するグラフです.

    ペテルセングラフ

    計算機におけるグラフの表現

    計算機上でグラフを扱うか, つまりグラフの符号化について述べておきます. 当然ながら良い符号化というものは, 目的に応じて変わりますし, グラフに付加的な性質がある場合には一般の場合よりも賢い符号化があり得ます. ですが, 一般的にグラフを計算機上で扱う際に最も使用されるグラフを保持する方法は隣接リスト(adjacent list)と呼ばれる方法でしょう. 隣接リストとは, 各頂点に対してそれに隣接する頂点を管理するデータ構造になります. 例えば \(C_4\) を例に見てみましょう.

    \(C_4\)

    このとき隣接リストでは各頂点に隣接する頂点を保持するので, 例えばPythonでは以下のようなリストで表現できます.

    [[1, 3], [0, 2], [1, 3], [0, 2]]

    隣接リストは各辺に対して, その辺の2つの端点がもう片方の端点に隣接しているという情報を保持するだけなので, 一般にグラフ \(G=(V,E)\) に対して, 隣接リストの保持に必要な空間は \(O(|V|+|E|)\) words 1程度になります.

    これは, 例えば隣接行列を保持する場合には \(O(|V|^2)\) words 程度必要なので, \(|E|\ll |V|^2\) のときは隣接行列に比べて非常に効率的になっていることに注意してください.

    最後にいくつか問題を用意しています. グラフをどのような構造で保持すれば効率よく解くことができるか考えてみてください.

    演習問題

    問題の中には単に理解を試すためのものと, 定理の巧妙な使い方を学ぶためのものがあります. なお, 解かなくても次の記事を読むに際して支障はないと思います. また, 演習問題は適宜加筆していくつもりなので, 順番は先に加えた順番になってしまっています.

    なお, 新しい演習問題や演習問題の順番等の変更に関する提案は常に受け付けています.

    問題1

    完全グラフ \(K_n\), 閉路グラフ \(C_n\), キューブグラフ\(Q_n\), クネーザーグラフ \(KG_{n,k}\) がすべて正則グラフであることを示し, その次数を求めてください.

    解答
    • \(K_n\) は \(n-1\)-正則グラフ.
    • \(C_n\) は 2-正則グラフ.
    • \(Q_n\) は \(n\)-正則グラフ.
    • \(KG_{n,k}\) は \(\binom{n-k}{k}\)-正則グラフ.

    問題2

    完全グラフ \(K_n\), 閉路グラフ \(C_n\), キューブグラフ\(Q_n\), クネーザーグラフ \(KG_{n,k}\) の辺の総数を求めてください.

    解答

    一般に \(n\) 頂点の \(d\)-正則グラフ \(G=(V,E)\) の辺の総数は握手補題から,

    \[|E|=\frac{1}{2}\sum_{v\in V}\deg_G(v)=\frac{nd}{2}\]

    であるので,

    • \(K_n\) の辺の総数は \(\frac{n(n-1)}{2}\).
    • \(C_n\) の辺の総数は \(n\).
    • \(Q_n\) の辺の総数は \(n2^{n-1}\).
    • \(KG_{n,k}\) の辺の総数は \(\frac{1}{2}\binom{n}{k}{n-k}{k}\).

    となる.

    問題3

    任意のグラフ \(G=(V,E)\) に対して, 次数が奇数の頂点は必ず偶数個存在することを示してください.

    解答

    \(Od\) で次数が奇数の頂点, \(Ev\) で次数が偶数の頂点を表すものとする. 握手補題から

    \[2|E|=\sum_{v\in V}\deg_G(v)=\sum_{v\in Od}\deg_G(v)+\sum_{v\in Ev}\deg_G(v)\]

    となるが, 定め方から \(v\in Ev\) に対して \(\deg_G(v)\) は偶数なので\(\sum_{v\in Ev}\deg_G(v)\) は偶数である.

    \[\sum_{v\in Od}\deg_G(v)=2|E|-\sum_{v\in Ev}\deg_G(v)\]

    より, 右辺は偶数なので左辺も偶数であり, 各\(v\in Od\) に対して \(\deg_G(v)\) は奇数より, \(|Od|\) が偶数でなければならない.

    問題4

    あるパーティーには2025人が参加している. このとき, パーティーに参加している人のうちちょうど偶数人の人と知り合いであるようなパーティーの参加者が存在することを示してください. ただし, 自分自身は自分自身の知り合いではないとします.

    解答

    ノードをパーティーの参加者, 辺をお互いが知り合いであるときに結ぶものとすれば, 参加人数が奇数なので, 握手補題からこのグラフで偶数次数のノードが存在する. このノートに対応する参加者がちょうど偶数人と知り合いである.

    問題5

    グラフ \(G=(V(G),E(G))\) に対して, \(G\) の 線グラフ(line graph) \(L(G)=(V(L(G)),E(L(G))\) とは, 頂点集合が\(G\) の辺集合 \(V(L(G))=E(G)\) であり, 相異なる\(e,f\in E(G)\) に対して, \(\partial e\cap\partial f\neq\emptyset\), すなわち端点を共有する時かつそのときに限り\(ef\in E(L(G))\) となるとして定まるグラフとします.

    1. \(L(K_3)\) が \(K_3\) に同型であることを示してください.
    2. グラフ\(G\) で \(L(G)\) が \(K_3\) に同型なグラフは \(K_3\) 以外に存在するかどうか考えてください.

    問題6

    グラフ \(G=(V,E)\) に対して, \(G\) の線グラフを\(L(G)\), 隣接行列を\(A_G\), 接続行列を\(B_G\) と書くとき,

    \[A_{L(G)}=B_G^\top B_G-2I_{|E|}\]

    が成立することを示してください. ここで非負整数 \(m\) に対して \(I_m\) で \(m\) 次単位行列を指すものとします.

    問題7

    グラフ \(G=(V,E)\) が \(d\)-正則であれば, 以下の式が成立することを示してください.

    \[B_GB_G^\top = A_G+dI_{|V|}\]

    なお, 記号は問題6と同じです.

    問題8

    この問題ではグラフ \(G=(V,E)\) に対して, その隣接行列 \(A_G\) の成分を\(V\times V\) に添え字づける, つまり\(A_G=(a_{uv})_{u,v\in V}\) とし, \(uv\in E\) かつそのときに限り \(a_{uv}=1\), そうでないとき \(a_{uv}=0\) とします.

    1. 任意の正整数\(n\) と \(u,v\in V\) に対して, \(A_G^n\) の \((u,v)\) 成分は \(u,v\) を端点とする \(G\) 上の長さ \(n\) の歩道の総数であることを示してください.
    2. \(A_G\) を実行列と考えます. このとき, \(A_G\) は対称行列なので, その固有値はすべて実数になります. 固有値の中で最大のものを\(\mu_1\) とおいたとき, 次式が成立することを示してください.
      \[\frac{2|E|}{|V|}\leq \mu_1\leq \max_{v\in V}\deg_G(v)\]
      特に \(G\) が正則であれば, 等号が成立することに注意しておきます.
    ヒント
    1. 帰納法.
    2. Courant-Fischerの定理として知られる以下の主張を用いてください:
      任意の\(n\) 次実対称行列 \(A\) に対して, その固有値のなかで最大のものを \(\lambda_1\) とすると, 次式が成り立つ.
      \[\lambda_1=\max_{\|x\|_2=1}x^\top Ax=\max_{x\neq 0}\frac{x^\top Ax}{x^\top x}\]
      ここで \(\|\cdot\|_2\) は\(\ell^2\)-ノルムである. なお, コンパクト集合上の連続関数の最大値の存在から上の最大値の記号は意味をもつ.

    問題9

    グラフ\(G,H\) に対して, \(\mathrm{Hom}(G,H)\) で \(G\) から \(H\) への準同型写像全体の集合を指すものとします. さらに \(\mathrm{Aut}(G)\) でグラフ \(G\) から \(G\) 自身への同型写像全体を指すものとします.

    1. 任意のグラフ \(G\) に対して, \(|\mathrm{Hom}(K_2,G)|=2|E(G)|\) が成立することを示してください. ここで \(K_2\) は \(n=2\) としたときの完全グラフ \(K_n\) のことです.
    2. \(\mathrm{Aut}(G)\) が合成について群をなすことを示してください.
    3. 同型でないグラフ\(G,H\) であって, \(\mathrm{Aut}(G),\mathrm{Aut}(H)\) が群として同型であるものを一つ見つけてください.

    プログラミング演習

    問題0001 Is Adjacent?

    採点システムへのリンクはこちら.

    問題:

    \(n\) 頂点, \(m\) 辺からなる無向単純グラフ \(G=(V,E)\) と, 正整数 \(Q\) が与えられます. グラフ \(G\) の頂点集合は \(V=\{0,1,\ldots,n-1\}\) からなるとします.

        \(Q\) 個のクエリ \((*)\) が与えられるので, それらにすべて解答してください.

        \((*)\) \(G\) の頂点 \(x,y\in V\) が与えられるので, \(xy\in E\) であれば「Yes」を, そうでなければ「No」を答えてください.

    制約:

    • \(1\leq n\leq 2\times 10^5\)
    • \(1\leq m\leq 4\times 10^5\)
    • \(1\leq Q\leq 4\times 10^5\)
    • \(n,m,Q\) は整数

    問題0002 Journey of a Walker

    採点システムへのリンクはこちら.

    問題:

    \(n\) 頂点, \(m\) 辺からなる無向単純グラフ \(G=(V,E)\) と正整数 \(k,Q\) が与えられます.

        グラフ \(G\) の頂点集合は \(V=\{0,1,\ldots,n-1\}\) からなるとします.

        \(Q\) 個のクエリ \((*)\) が与えられるので, それらにすべて解答してください.

        \((*)\) \(x,y\in V\) が与えられるので, \(x\) から \(y\) への歩道の中で長さがちょうど \(k\) であるようなものの総数を \(1000000007\) で割った余り \(r\) を \(0\leq r<1000000007\) の形で解答してください.

        ここで, \(1000000007\) は素数です.

      制約:

    • \(1\leq n\leq 100\)
    • \(1\leq m\leq \frac{n(n-1)}{2}\)
    • \(1\leq k\leq 1\times 10^9\)
    • \(1\leq Q\leq 4\times 10^5\)
    • \(n,m,k,Q\) は整数

    脚注:

    1. ここでwordsはメモリの基本単位を指しています. これは現在の普通の家庭用コンピュータであれば, 64bitだと思いますが, そういったアーキテクチャや実行環境に左右されないような書き方をしています. この辺の計算モデルに関する細かな話はいずれ記事にしても良いかなと思っていますが, ここでは何となくで受け取ってもらっても特に支障はないと思われます. ↩︎